would a growth potion need to be in a larger bottle than a shrinking potion? at first i thought no, that’s silly. but then i thought, what if it’s not silly?

since you can’t absorb all of a potion instantly, the first part to enter your digestive system will take effect before absorption of later parts of the potion

so, in the case of a growth portion, you will be larger by the time the final portion of the potion enters the bloodstream

the larger you are, the less potency most drugs will have on you; importantly, the final less potent portion of the potion contributes a disproportionately small portion of your growth compared to the more potent primary portion of the potion

first i’ll try to model the problem without worrying about dilution and metabolism, then i expect i’ll need to use integrals or something

a simple model is just to map a percentage height increase to a volume consumed (regardless of prior growth)

tex practice

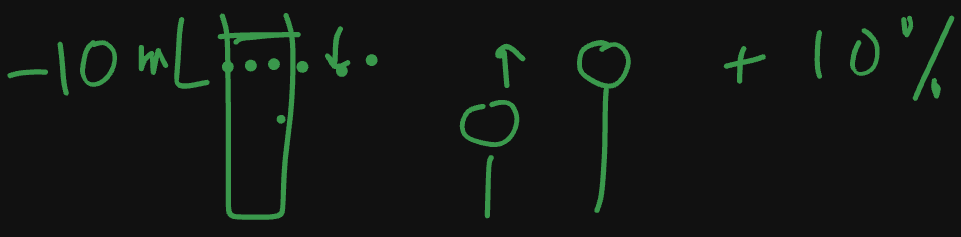
volume decreases at constant 10 mL per sip height increases by 10% per sip (r)

sip (n)	volume sipped (n • v)	height (h)
0	0	100
1	10	110
2	20	121
3	30	133.1

$$h_f=h_i\cdot (1+r{)}^n$$

confirmation

$$\begin{array}{rl}{h}_f& =100\cdot (1+0.1{)}^3\\ & =100\cdot 1.331\\ & =133.1\end{array}$$

and for the full bottle:

$$\begin{array}{rl}{h}_f& =100\cdot (1+0.1{)}^{10}\\ & =100\cdot 2.594\\ & =259.4\end{array}$$

so this is just an interest problem???

time to break out continuous interest

$$\begin{array}{rl}t& \to n\\ P_0& \to h_i\\ P(t)& \to h_f\\ r& \to 1+r\end{array}$$ $$h_f=h_i{e}^{rn}$$

using this to find the height increase from the entire bottle:

$$\begin{array}{rl}{h}_f& =100\cdot e^{0.1\cdot 10}\\ & =100\cdot e\\ & =271.828\end{array}$$

and this is where there interest analogy hits a snag. drinking the same amount of growth potion should cause the same amount of growth. so we need to know if the given potency of the potion assumes continuous or discrete compounding, or put other such bounds so that we could confidently label the bottle as providing either 271% or 259% growth or something else, since it can’t be both.

the tangible difference in accounting is about when the interest due is reassessed. in this problem, the ‘interest’ is predetermined, and the choice of formula must not change it.

modeling in terms of sips is probably not ideal

for a bottle which is advertised as providing 300% of growth in a 100 mL dose, where $n=1$ as this disregards sips:

$$\begin{array}{rl}{h}_f& =h_i{e}^{n(r+1)}\\ r+1& =n^{-1}\ln \frac{h_f}{h_i}\\ r+1& =1\cdot \ln \frac{300}{100}\\ r+1& =\ln 3\\ r& =1.0986-1\\ r& =9.86\%\end{array}$$

what??? how would a rate of 9.86% cause 300% growth in a single dose? deeply misunderstanding something here

to be continued